Comment faire de la pseudoscience avec des données réelles : une critique des arguments statistiques de John Hattie dans Visible Learning par un statisticien
Les travaux de John Hattie sur l’enseignement comportent, semble-t-il, ce qu’il y a de plus complet comme synthèse des recherches dans le domaine de l’éducation. Son livre, Visible Learning (Hattie, 2008), est considéré par plusieurs comme une Bible ou un Saint-Graal : « Lorsque ce travail est paru, certains commentateurs l’ont décrit comme le Saint-Graal de l’éducation, ce qui n’est sans doute pas une trop grande hyperbole » (Baillargeon, 2014, paragr. 13).
Pour ceux qui sont peu habitués à décortiquer les chiffres, une telle synthèse parait en effet être un travail colossal et minutieux, ce qui donne des apparences de validité scientifique. Pour un statisticien accoutumé à la méthode scientifique, de l’élaboration des questions à l’interprétation des analyses, les apparences ne suffisent pas. Il faut regarder en profondeur, et sous l’œil d’un expert, le château du Roi pêcheur qui garde le Graal devient un fragile château de cartes qui s’écroule rapidement. Cet article offre une critique de la méthodologie utilisée par Hattie du point de vue d’un statisticien. On peut conter des histoires à partir de données réelles pour vulgariser les résultats, mais ces histoires ne doivent pas tomber dans la fiction. Il faut donc absolument qualifier la méthodologie de Hattie de pseudoscience. Le chercheur néo-zélandais a évidemment des intentions louables, qu’on décrit en premier lieu. Les bonnes intentions n’empêchent pas moins des erreurs majeures dans Visible Learning, erreurs dont on parle en deuxième lieu. Ce processus d’analyse mène ensuite à une liste de questions qu’un chercheur devrait se poser en examinant des études et enquêtes basées sur des analyses de données, incluant les méta-analyses. Après, pour mieux comprendre, on présente des exemples concrets démontrant que le d de Cohen (la mesure de base derrière les effets d’ampleur, effect sizes, de Hattie) ne peut tout simplement pas être utilisé comme une mesure universelle d’impact. En dernier lieu, afin que la quête ne reste pas inachevée, on offre des pistes de solution dans le but de démythifier, démystifier et encourager la bonne utilisation des statistiques dans les sciences de l’éducation.
LES INTENTIONS DE JOHN HATTIE
L’idée de base des recherches de Hattie, c’est-à-dire de trouver des outils d’enseignement qui fonctionnent en utilisant des données recueillies scientifiquement, n’est pas mauvaise en soi. Le désir de rigueur et de données concrètes est essentiel pour décrire l’impact des mesures sur le succès dans l’apprentissage et l’enseignement. Hattie fait appel à des méta-analyses ; ce sont des méthodes statistiques relativement complexes utilisées fréquemment, entre autres, dans le domaine des recherches en santé et en médecine. La taille de sa synthèse paraît impressionnante : plus de 800 méta-analyses, comportant plus de 50 000 études et des millions d’individus. Avec au départ plus de 135 « effets d’ampleur », il semble pouvoir mesurer toute une panoplie d’interventions pouvant améliorer l’apprentissage. Hattie n’a pas peur des chiffres, ce qui n’est apparemment pas si fréquent parmi les chercheurs dans le domaine de l’éducation ; cela donne donc apparence de rigueur scientifique à ses travaux. Par conséquent, pour un statisticien, cela semble un très bon départ.
Malheureusement, en lisant Visible Learning et les ouvrages subséquents de Hattie et de son équipe, quiconque s’y connait en matière de données probantes et de méthodologie statistique déchante très rapidement. Pourquoi ? Parce qu’on ne peut pas recueillir des données n’importe comment ni les analyser ou les interpréter n’importe comment. Or, ceci résume la méthodologie réelle du chercheur néo-zélandais. Croire Hattie, c’est avoir un angle mort dans ses outils de pensée critique quand vient le temps d’évaluer la rigueur scientifique. Faire la promotion de ses travaux c’est malheureusement tomber dans l’apologie de la pseudoscience. Enfin, persister à défendre Hattie après avoir pris connaissance de la critique sérieuse de sa méthodologie constitue de l’aveuglement volontaire.
ERREURS MÉTHODOLOGIQUES
Fondamentalement, la méthode de Hattie n’est pas statistiquement sophistiquée et se résume à faire des moyennes de chiffres et calculer des écarts types dont il ne se sert pas vraiment. Il utilise des diagrammes à barres (pas d’histogrammes) et est capable de se servir d’une formule qui convertit une corrélation en d de Cohen (on la retrouve dans Borenstein, Hedges, Higgins et Rothstein, 2009), sans comprendre les prérequis pour que ce genre de conversion soit valide. Il est coupable de nombreuses erreurs, mais ses principales correspondent à deux des trois erreurs majeures en science citées par Allison, Brown, George et Kaiser (2016) dans Nature :
1. Des erreurs de calcul dans les méta-analyses
2. Des bases de comparaison inappropriées
La plus flagrante de ses erreurs de calcul est le cas des common language effects (CLE, effets de langage commun), qui prennent la forme d’une probabilité. Remarquée en 2012 par des chercheurs norvégiens (Topphol, 2012), elle est flagrante au point de donner des probabilités négatives ou supérieures à 100 %. Hattie n’aurait eu qu’à faire un petit tableau (voir le Tableau 1) pour aider le lecteur (et lui-même) à voir la relation entre l’effet d’ampleur et CLE.
Tableau 1. Correspondance entre des valeurs choisies de d de Cohen et les CLE équivalents
|
d |
0,00 |
0,20 |
0,40 |
0,60 |
0,80 |
1,00 |
1,20 |
1,40 |
2,00 |
3,00 |
|
CLE |
50 % |
56 % |
61 % |
66 % |
71 % |
76 % |
80 % |
84 % |
92 % |
98 % |
Ne pas remarquer la présence de probabilités négatives est d’une grossièreté énorme pour quiconque a suivi au moins un cours de statistique dans sa vie. Pourtant, ce n’est qu’un symptôme d’un manque total de rigueur scientifique, et la moindre des erreurs de raisonnement dans Visible Learning. Si Hattie avait pris la peine de consulter un statisticien d’expérience, il n’aurait pas commis pareille bourde : selon R. A. Fisher, consulter un statisticien après qu’une expérience soit terminée est souvent semblable à demander une autopsie. Il pourra peut-être dire comment l’expérience a échoué (cité dans Allison et coll., 2016).
Les autres erreurs de calcul ne sont pas tant numériques que liées aux bases de comparaison inappropriées et à l’absence de rigueur méthodologique. Hattie croit qu’on peut comparer des effets d’ampleur parce que le d de Cohen est une mesure sans unité et il donne deux exemples de calculs :

Ces deux types d’effets ne sont pas équivalents et ne peuvent être comparés directement. Nous y reviendrons plus tard. D’ores et déjà, un statisticien se posera plusieurs questions et aura un doute énorme sur l’ensemble de la méthodologie de Visible Learning et ses dérivés.
LES QUESTIONS À POSER
S’il y a une morale à retenir de Perceval, ou le Conte du Graal, roman inachevé de Chrétien de Troyes, c’est qu’il ne faut pas hésiter à poser des questions. Confronté à tout ensemble de données, il faut toujours savoir quelle est la question principale à laquelle on veut répondre. Lié à cela, il faut savoir quelles sont les variables mesurées et la façon dont les mesures ont été obtenues. Quelle est la population ciblée ? Comment l’échantillon a-t-il été recueilli ? Lorsqu’il y a des groupes comparés, et surtout lorsqu’on mesure une intervention, par exemple, sur un groupe expérimental par rapport à un groupe témoin, il faut se demander comment les individus ont été répartis. Si les groupes ne sont pas répartis de façon aléatoire, les différences observées peuvent être dues à la nature des groupes au départ et non pas à un traitement ou une intervention. À quelle échelle a-t-on mesuré les variables (individuelle, groupe, école, provinciale, nationale) ? Toutes ces questions permettront de comprendre ce qu’une étude ou méta-analyse mesure vraiment et dans quel contexte. Sans avoir le contexte précis, il est facile de faire des erreurs d’interprétation et ces erreurs se révèlent parfois très coûteuses. La catastrophe de la navette Challenger en est un exemple : la sélection des données menant à l’autorisation de décollage a fait croire en l’absence d’une relation entre la température et le risque d’accident, parce que les cas sans incident avaient été exclus (Kennet et Thyregod, 2006).
Hattie parle de succès dans l’apprentissage, mais parmi ses méta-analyses, comment mesure-t-on ce succès ? L’effet sur les notes n’est pas le même que l’effet sur le taux de diplomation. Un effet sur la perception d’apprentissage ou sur l’estime de soi n’est pas nécessairement lié au « succès scolaire » et ainsi de suite. Une étude sur une courte période ne mesurera pas la même chose qu’une étude basée sur un an ou plus. Et, bien sûr, on ne peut pas dire que ce qui est observé chez des élèves du primaire vaut également au secondaire ou à l’université. Il en va de même pour sa façon de regrouper des influences sous une même étiquette sans présenter de critères définis. Par exemple, l’effet du genre rapporté par Hattie est en fait une moyenne de différences entre les garçons et les filles dans l’ensemble des études recueillies, peu importe la durée, le niveau ou les populations.
UNE MESURE UNIVERSELLE QUI N’EXISTE PAS
En gros, Hattie fait des moyennes qui n’ont aucun sens. L’exemple classique d’une telle moyenne est de dire que, si j’ai la tête dans le four et les pieds au congélateur, en moyenne, je suis très confortable. Un autre exemple humoristique de mauvaise moyenne est de dire que la personne moyenne a un testicule et un ovaire et donc est hermaphrodite. On ne dirait pas de quelqu’un faisant cet énoncé qu’il détient le Saint-Graal des recherches en biologie, et pourtant c’est exactement ce que Hattie fait en regroupant toutes les différences de genre sous un même effet. Cela vaut aussi pour tous ses autres regroupements, que ce soit les sources de contributions « majeures » (l’élève, la maison, l’école, l’enseignant, le programme, ou l’enseignement), ou les influences « individuelles », comme la « maladie », qui regroupe des problèmes disparates comme le cancer, le diabète, l’anémie falciforme et les troubles intestinaux. Il va sans dire que certaines sous-influences sont beaucoup plus rares que d’autres.
Le problème fondamental ici est que tout effet d’ampleur, malgré l’absence d’unité, est une mesure relative, qui comporte une comparaison à un ensemble, groupe ou population de base, même si elle peut être implicite. Comparer deux groupes indépendants n’est pas la même chose que comparer les notes avant et après une intervention auprès d’un même groupe. C’est le premier choix tout à fait arbitraire que Hattie fait tout en l’ignorant complètement. Le choix de la base de comparaison définit la direction (le signe positif ou négatif) de l’effet d’ampleur. Dans son cadran, Hattie dit que les effets négatifs sont des effets néfastes (reverse effects), ce qui n’est pas nécessairement le cas puisque, souvent, la comparaison est arbitraire. Dirait-on que les différences dans le succès scolaire en faveur des filles sont mauvaises, alors que celles en faveur des garçons sont bonnes ?
L’effet de la taille des classes (sous la barre « significative » selon Visible Learning, qui est 0,4) est positif et on suppose qu’on compare de petites classes à de plus grandes classes (le succès scolaire est plus grand dans les classes plus petites). On aurait pu comparer les grandes classes aux petites, et l’effet aurait été négatif (les grandes classes ont moins de succès que les petites), et l’interprétation que fait Hattie (la taille des classes n’a pas un impact important) deviendrait complètement différente, étant donné qu’un impact négatif est considéré comme étant mauvais.
Il en va de même pour le statut socio-économique. L’effet est grand (0,59), mais puisque Hattie ne peut changer le statut socio-économique des élèves, il ne s’en préoccupe pas. La comparaison implicite est que les élèves issus de milieux plus riches ont plus de succès que les élèves plus pauvres et, donc, la base de comparaison est constituée des élèves plus pauvres. On pourrait tout aussi bien comparer les plus pauvres aux plus riches et, parce que les défavorisés ont moins de succès scolaire, l’effet du statut socio-économique deviendrait -0,59, le plus négatif de tous, si on ne change aucun autre. Organiser le système d’éducation de façon à atténuer le plus possible l’effet des inégalités sociales devient alors une intervention qui mérite d’être étudiée, en s’inspirant peut-être de la Finlande, par exemple, où cette approche semble avoir du succès, du moins, du point de vue des tests PISA (Reinikainen, 2012).
L’autre choix arbitraire est le regroupement pour faire des effets moyens. Là, en plus de mêler des dimensions multiples et incompatibles, Hattie confond deux populations distinctes : la population des influences sur le succès scolaire et la population des études sur ces influences. Comme analogie, on pourrait énumérer tout ce qui se vend en épicerie selon le prix et dire que ce sont les produits de la mer qui ont le plus d’impact sur le panier d’épicerie, parce que le caviar est hors de prix. Évidemment, vu que le consommateur moyen n’achète que très rarement, voire jamais du caviar, il faudrait tenir compte d’une pondération des prix qui reflète les quantités de chaque produit que le consommateur achète vraiment pour s’approcher de la réalité. Retournons à l’exemple de l’impact du genre sur le succès scolaire. Il est 0,12 selon Hattie, donc en faveur des garçons. Si ce chiffre était représentatif d’une quelconque réalité, cela voudrait dire que les garçons ont un peu plus de succès à l’école que les filles. Ce n’est pas le cas au Québec ni dans la plupart des pays industrialisés (Legewie et DiPrete, 2012).
L’interprétation que Hattie fait des effets n’est donc pas la moindrement objective. Comme mentionné plus tôt, selon son cadran, les effets sous zéro sont néfastes, entre 0 et 0,4 on passe des effets « de développement » aux effets « des professeurs » et au-dessus de 0,4, on a la zone d’effets désirés. Il n’a aucune justification pour faire un tel classement. D’abord, il n’a pas de point de référence de base universel pour centrer son effet nul et parler de développement. Une personne seule et sans instruction peut-elle apprendre d’elle-même de façon mesurable ? Si les effets dus aux professeurs tombent entre 0,15 et 0,4, pourquoi l’impact de la connaissance de la matière par l’enseignant est-il seulement de 0,09 ? Peut-on dire que quelqu’un désapprend lorsqu’un effet est négatif ? Devrait-on parler de science infuse chez quelqu’un qui n’a pas l’anémie falciforme ou qui est né à terme, étant donné que Hattie choisit, au final, de mettre un effet positif à l’absence de maladie ?
Enfin, Hattie confond corrélation et causalité en cherchant à tout réduire à un effet d’ampleur. Selon le contexte, au cas par cas, on peut effectivement passer d’une corrélation à un d de Cohen (Borenstein et coll., 2009):
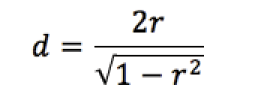
mais il faut absolument savoir dans quel espace mathématique se situent les données pour passer d’une échelle à l’autre. L’utilisation de cette formule est hyperhasardeuse, car elle explose rapidement lorsque la corrélation tend vers un, et donne des effets relativement forts pour des corrélations faibles. Il suffit d’une corrélation de ,196 pour atteindre la zone d’effet désiré de Visible Learning. Dans un modèle de régression linéaire simple, cela se traduit par 3,85 % de la variabilité expliquée par le modèle pour 96,15 % de bruit aléatoire non expliqué, donc un très faible impact réel. C’est avec cette formule que Hattie obtient, entre autres, son effet de la créativité sur le succès scolaire (Kim, 2005), qui est en fait une corrélation entre des résultats de tests de quotient intellectuel et des tests de créativité. C’est aussi par des corrélations qu’il obtient le soi-disant effet des notes autorapportées, l’effet le plus fort dans la mouture initiale de Visible Learning. Or, cela s’avère plutôt un ensemble de corrélations entre des notes rapportées et des notes réelles, ensemble qui ne mesure pas le moindrement une augmentation du succès scolaire entre des groupes où l’on utilise des notes autorapportées et des groupes où l’on ne fait pas ce genre d’auto-examen.
Exemple : trois façons de calculer un effet d’ampleur
Il existe une panoplie de façons valides d’analyser chaque ensemble de données ; chacune de ces façons illustre un aspect différent du problème étudié. C’est pour cela qu’il faut absolument s’assurer d’être à la bonne échelle, dans la même perspective, lorsque vient le temps de faire des méta-analyses ou des moyennes d’effets d’ampleur. On peut considérer l’exemple suivant : quatre groupes indépendants et identiquement distribués de loi normale (avec, par exemple, une moyenne de 75 et un écart type de 5). Les quatre groupes suivent un cheminement identique avec la méthode d’enseignement « standard ». Pour le prochain module d’enseignement, chaque groupe est assigné aléatoirement à une nouvelle méthode d’enseignement parmi trois, que l’on numérotera 1, 2 et 3, et un groupe continuera avec la méthode standard, étiquetée méthode 0. À la fin du module, tous les groupes passeront un test identique et on fera une comparaison pour mesurer un effet d’ampleur. Supposons que l’augmentation des notes suit une loi normale et que, en moyenne, la méthode i augmente les notes individuelles de i point avec un écart type de i. Les notes du groupe témoin ne changent pas (effectivement, augmentation de 0 avec écart type 0).
On utilisera les trois formules d’effets d’ampleur pour, comme Hattie, faire un classement des méthodes d’enseignement pour trouver la « meilleure ». On peut, en premier lieu, comparer les groupes expérimentaux au groupe témoin (a). Par la suite, on regardera les notes avant et après pour chaque groupe (b), et enfin, on utilisera la corrélation entre la note avant et après pour chaque groupe et convertir en d de Cohen (c). Les effets d’ampleur sont dans le Tableau 2.
Tableau 2. Comparaison de différentes méthodes de calcul d’effet d’ampleur
|
Groupe |
(a) |
(b) |
(c) |
|
Témoin |
0,00 |
N/A |
Infini |
|
Méthode 1 |
0,14 |
1,00 |
10,00 |
|
Méthode 2 |
0,27 |
1,00 |
5,00 |
|
Méthode 3 |
0,39 |
1,00 |
3,33 |
Selon les effets d’ampleur mesurés par la formule (a), la méthode 3 est la meilleure, et la seule qui se trouve presque dans la zone d’effet désiré. La formule (b) porte à croire que les trois méthodes sont équivalentes (même si dans les faits, l’effet réel varie d’une méthode à l’autre), mais toutes sont bien haut dans la zone d’effet désiré. Finalement, selon la formule (c), la méthode standard est infiniment meilleure que les autres, et l’ordre est complètement inversé par rapport à la formule (a). Que se passe-t-il ?
La formule (a) compare des groupes indépendants entre eux et inclut donc le bruit dû à la variabilité des groupes. On essaie de départir les quatre courbes normales illustrées dans la Figure 1, qui se chevauchent passablement. Et on a la chance que les groupes aient été identiques avant et que les méthodes aient été attribuées au hasard, donc les effets mesurés sont ceux des méthodes d’enseignement.
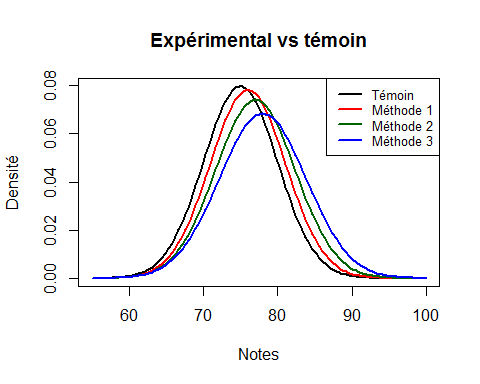
Figure 1. Répartition des notes selon le groupe
Puisque la formule (b) mesure l’augmentation des notes pour chaque groupe, on compare chaque groupe à lui-même, ce qui fait disparaître une source de bruit (la différence entre les groupes). L’effet mesuré est plus « pur », mais on perd la capacité de comparer les groupes entre eux, car l’écart type change d’un groupe à l’autre, et en divisant l’augmentation moyenne par l’écart type, on a perdu une dimension. Les courbes de loi normale des changements de notes sont représentées dans la Figure 2. Bien que ces courbes soient très différentes, les effets mesurés sont identiques.
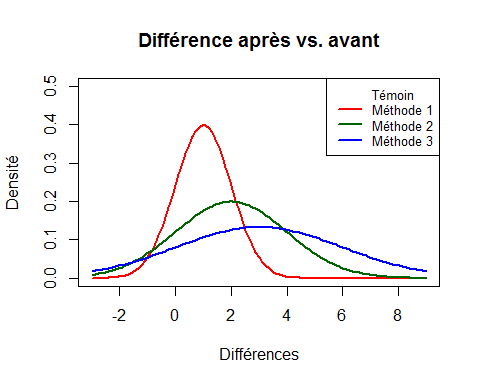
Figure 2. Répartition des différences entre les notes après et avant selon le groupe
Finalement, comme c’est le cas pour plusieurs effets basés sur des corrélations, la formule (c) ne mesure pas l’augmentation des notes (l’effet de la méthode d’enseignement), mais le bruit autour de ce changement. Plus l’écart type de l’augmentation est grand, plus la corrélation est faible et, donc, la conversion en d donne un effet plus faible là où l’écart type est plus grand (mais des effets énormes comparés aux formules (a) et (b)).
SOLUTION : CONSULTER UN STATISTICIEN
Les exemples ci-dessus ne décrivent qu’une partie des erreurs fondamentales de raisonnement dans Visible Learning. On pourrait passer un temps fou à décortiquer chaque méta-analyse utilisée, à évaluer à quel point il y a des erreurs de calcul et d’interprétation et à décrire les limites réelles des analyses d’origine. L’espace manque aussi pour expliquer la complexité et les subtilités d’une modélisation raisonnable d’effets d’intervention à partir de différentes études observationnelles ou expérimentales, des questions de relations dose-effet, de situations géographiques et temporelles. Tout cela est complètement perdu lorsqu’on décide de tout réduire en un seul chiffre qui est insuffisant pour représenter la réalité.
En somme, il est clair que John Hattie et son équipe n’ont ni les connaissances ni les compétences pour faire des analyses statistiques valides. Personne ne devrait imiter cette méthodologie et cette façon de faire, parce qu’on ne doit jamais accepter la pseudoscience. C’est fort malheureux parce qu’il serait possible de faire de la véritable science avec les données de centaines de méta-analyses.
La statistique et la science des données modernes offrent une panoplie d’outils qui permettent de mieux comprendre des données recueillies avec rigueur, et en extraire des conclusions utiles et applicables. Il va sans dire que le développement du système d’éducation doit être analysé de façon scientifique et pour cela, la solution reste la même que celle proposée par Fisher (cité dans Allison et coll., 2016) il y a plusieurs décennies : on doit consulter un statisticien avant de recueillir des données. Et pendant la collecte de données. Et après. Mais surtout, à chaque étape d’une étude. Il ne faut pas se laisser impressionner par la quantité de chiffres et la taille des échantillons ; il faut se préoccuper de la qualité du plan d’expérience et de la validité des données recueillies.
Pour tout cela, il faut faire appel à des statisticiens d’expérience qui sauront garder l’œil ouvert et l’esprit critique. Toute université qui se respecte a un service de consultation statistique pour soutenir la recherche scientifique. Il est aussi possible d’obtenir ces services par des compagnies ou consultants privés. Il n’y a aucune raison pour les facultés d’éducation de ne pas faire appel à de tels services. Il est impératif de le faire, car, si l’on se fie à Indiana Jones et la dernière croisade, les conséquences de mal choisir son Graal sont fort tragiques.
références
Allison, D. B., Brown, A. W., George, B. J. et Kaiser, K. A. (2016). Reproducibility: A tragedy of errors. Nature, 530, 27-29.
Baillargeon, N. (2014, 23 février). Visible learning [Billet de blogue]. Repéré à https://voir.ca/normand-baillargeon/2014/02/23/visible-learning/
Borenstein, M., Hedges, L., Higgins, J. et Rothstein, H. (2009). Introduction to meta-analysis. Hoboken, NJ : John Wiley & Sons.
Hattie, J. (2008). Visible learning: A synthesis of over 800 meta-analyses relating to achievement. Londres, Royaume-Uni : Routledge.
Kennet, R. et Thyregod, P. (2006). Aspects of statistical consulting not taught by academia. Statistica Neerlandica, 60(3), 396-411.
Kim, K. H. (2005). Can only intelligent people be creative? A meta-analysis. Prufrock Journal,
16(2-3), 57-66.
Legewie, J. et DiPrete, T. A. (2012). School context and the gender gap in educational achievement. American Sociological Review, 77(3), 463-485.
Reinikainen, P. (2012). Amazing PISA results in Finnish comprehensive schools. Dans H. Niemi, A. Toom et A. Kallioniemi (dir.), Miracle of education (p. 3-18). Rotterdam, Pays-Bas : Sense Publishers.
Topphol, A. K. (2012). Kan vi stole på statistikkbruken i utdanningsforskinga? [Peut-on se fier à l’usage des statistiques dans la recherche en éducation?]. Norsk Pedagogisk Tidsskrift, 95(6), 460-471.